EasyVent
EasyVent è il software di selezione Soler&Palau Ventilation Group. Questo selettore online ti accompagnerà dall'inizio del progetto, adattandosi alle modifiche che sipresenteranno strada facendo. Le principali funzionalità di cui potrai usufruire sono:
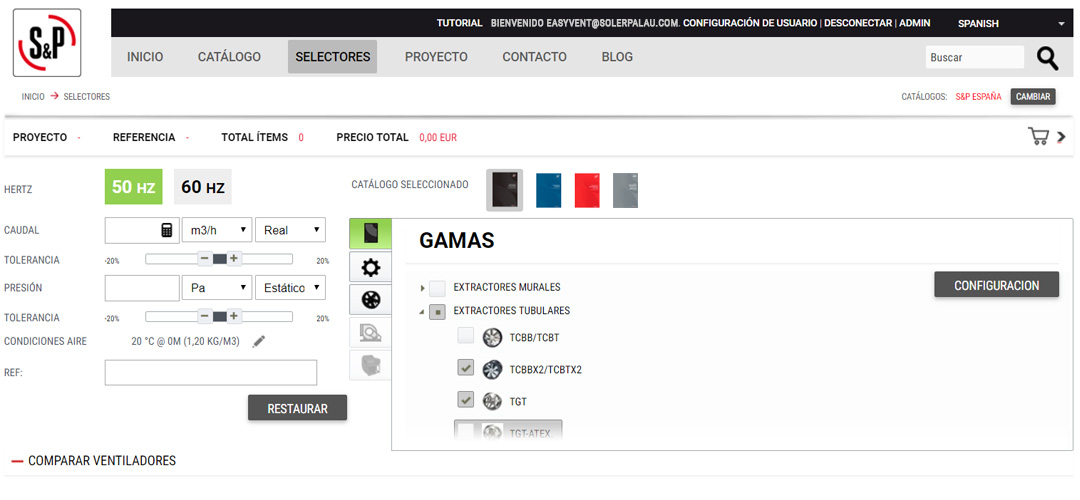
Selezione di ventilatori con il punto di lavoro richiesto:
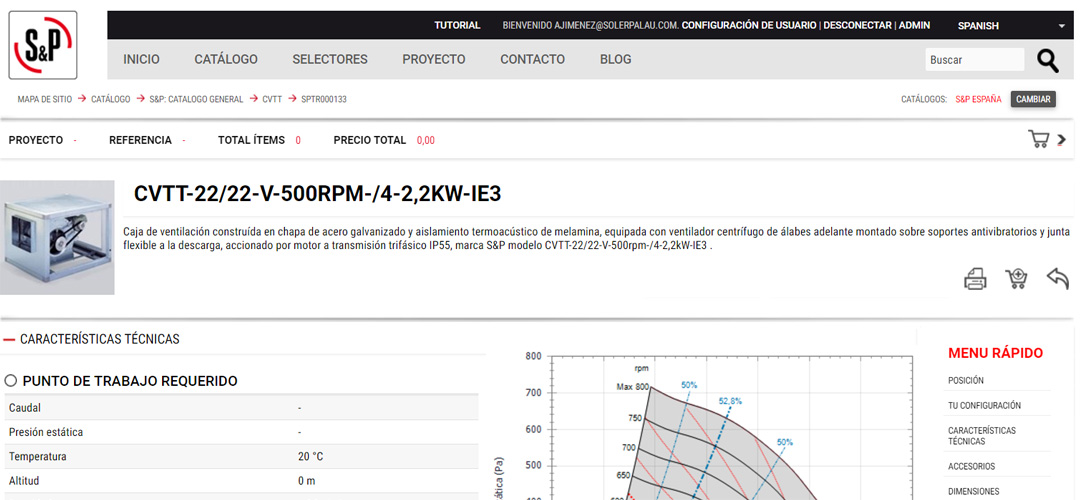
- Descrizione dettagliata del prodotto selezionato e indicazione sul punto di lavoro effettivo.
- Descrizione delle caratteristiche tecniche, consumo, efficienza, livello sonoro e SFP.
- Descrizione delle caratteristiche fisiche del prodotto come dimensioni, peso e modello 3D scaricabile in diversi formati.
Selezione di recuperatori di calore:
- Descrizione dettagliata del prodotto selezionato con indicazioni sulla sua configurazione specifica.
- Descrizione delle caratteristiche tecniche, consumo, efficienza, livello sonoro e SFP.
- Descrizione delle caratteristiche fisiche del prodotto come dimensioni, peso e modello 3D scaricabile in diversi formati.
Stampa di cataloghi personalizzati, schede tecniche di prodotti o progetti.
Aggiunta di accessori a prodotti.
Possibilità di pre-calcolo della portata.
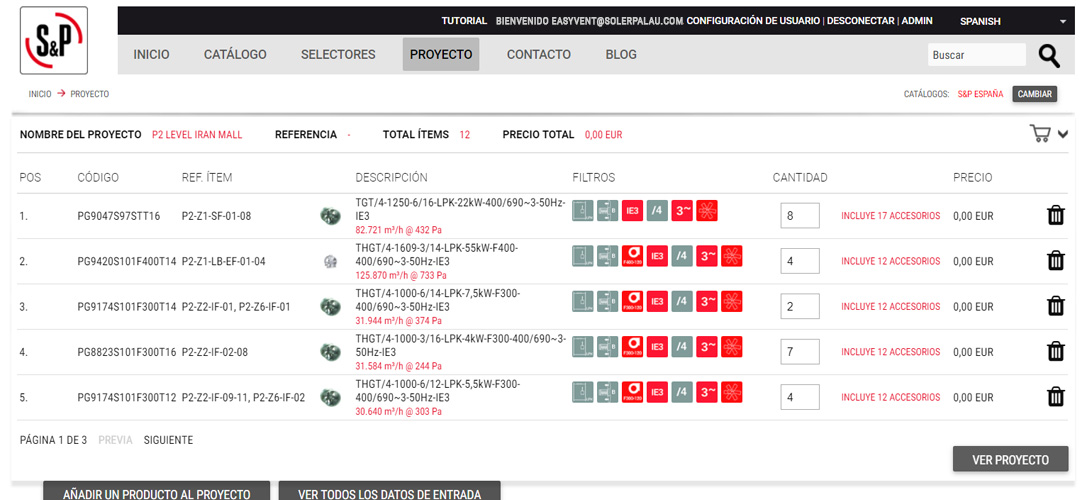
Creazione, aggiornamento e personalizzazione di un progetto di ventilazione:
- Strumenti di selezione multipla rapida.
- Raccolta di progetti con i prodotti accessibili in qualsiasi momento.
- Aggiunta del logo del progetto.
- Possibilità di riconfigurare un prodotto una volta aggiunto al progetto.
- Possibilità di rimpiazzare un prodotto per un altro se necessario.
Ottenere oggetti in formato BIM.
Schema dimensionale: visualizzazione in 3D del prodotto, possibilità di scaricare in formato CAD.
 Aspiratori da bagno
Aspiratori da bagno Estrattori da vetro o parete
Estrattori da vetro o parete Ventilatori in linea
Ventilatori in linea VMC
VMC Casse di ventilazione
Casse di ventilazione Torrini
Torrini Estrattori per cappe da cucina
Estrattori per cappe da cucina Ventilazione estiva
Ventilazione estiva Trattamento dell'aria
Trattamento dell'aria Riscaldamento
Riscaldamento Recuperatori di calore
Recuperatori di calore Asciugamani e asciugacappelli
Asciugamani e asciugacappelli Ventilatori elicoidali da parete
Ventilatori elicoidali da parete Ventilatori elicoidali tubolari
Ventilatori elicoidali tubolari Ventilatori centrifughi
Ventilatori centrifughi Estrazione fumi
Estrazione fumi Jet fan
Jet fan Ventilatori ATEX
Ventilatori ATEX Barriere a lama d'aria
Barriere a lama d'aria Sistemi di pressurizzazione
Sistemi di pressurizzazione Accessori di montaggio
Accessori di montaggio Accesori elettrici
Accesori elettrici Accessori per VMC
Accessori per VMC